В связи с критической рецензией на нашу статью считаем необходимым ответить на поставленные вопросы. Полагаем, что доводы рецензентов невозможно признать убедительными ни в одном из представленных ими положений. Запрошенное «аналитическое исследование сравнительной эффективности» актуариальных методов, которое, разумеется, имеется в статье, необоснованно отвергнуто, наша методика признана «ошибочной» без предоставления этому доказательств, а результаты расчетов, подводящие итоги исследования и подтверждающие справедливость наших выводов, вообще не приняты к рассмотрению.
Наша аргументация излагается по воспроизводимым ниже шести пунктам–вопросам рецензии и состоит в следующем:
Вопрос рецензентов N1
Нужно ли пропагандировать грубые актуариальные методы (анализ таблиц дожития), когда существуют более точные методы анализа выживаемости, основанные на первичных, не агрегированных данных?
«Более точный» метод E.Kaplan-P.Meier, (1958) "Product-Limit (PL) Estimate" именуемый также «актуариальным» (см., например, цитируемые нами работы проф. В.В. Двойрина), изложен самими E.Kaplan-P.Meier в нескольких модификациях. Кроме «PL- Estimate» существует его «грубое» актуариальное тождество -"Actuarial approximation of the PL-Estimate". При этом «approximation-тождество» имеет значение и как «приблизительная точность», что подтверждается результатами расчетов в одних и тех же примерах, и как «полное сходство», что подтверждается цитатой и соответствующими (одними и теми же) формулами. На это обстоятельство мы еще будем особо обращать внимание при ответе на вопрос-5 рецензентов. «Как PL, так и его актуариальное тождество основаны на одних принципах» (“Both the PL and the actuarial estimates … are based on the following general procedure” /E.Kaplan-P.Meier/):
(формулы1)
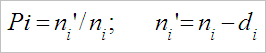
где: Рi показатель выживаемости интервала, ni- число наблюдений в начале интервала, ni’ –число наблюдений в конце интервала, di- число умерших. (Обозначения в этом тексте сделаны в соответствии с указаниями авторов рецензии, по E.Kaplan-P.Meier, с изменениями, внесенными самими рецензентами. В тексте направленной в Ваш журнал статьи обозначения сделаны в более часто употребляемых символах S.Cutler-F.Ederer).
Обращает внимание, что в формулах (1) показатель выживаемости временного интервала определяется отношением числа переживших этот интервал к числу наблюдавшихся в его начале. При этом – число случаев в конце интервала соответствует начальному числу за вычетом умерших. Иными словами – в основе «более точного» метода (PL) Estimate, а также всех его модификаций заключено предположение о том, что все выбывшие [l] больные доживут до конца интервала. Как очевидно, именно это предположение и приводит к неизбежному завышению выживаемости сравнительно с фактическими данными, причем наибольшему завышению, сравнительно с другими методами.
Отметим также, что применение самого "Product-Limit" метода затруднено тем немаловажным обстоятельством, что в реальной действительности именно «первичные точные данные» нередко оказываются недоступными. Источники информации (адресные бюро, онкодиспансеры, др.) могут иметь лишь сугубо «агрегированные» сведения. Например: «умер (выбыл) в таком-то году». Из разных источников могут поступить и сведения, к примеру о наступившем летальном исходе, с разницей в несколько месяцев. В этой связи именно расчеты с применением «грубого» актуариального тождества -"Actuarial approximation of the PL-Estimate", также как и его «скорректированной оценки» -"The adjusted-Observed [l/2] Estimate" в которой в расчет принимается 1./2 от числа выбывших (расчет также предложенный E.Kaplan-P.Meier). могут заменить неосуществимую процедуру "Product-Limit (PL) Estimate" Однако эти подробности отвлекают наше внимание от основного положения, имеющего наибольшее значение для проблемы надежности актуариальных расчетов по таблицам дожития, особо отмеченного в нашей статье, но парадоксально оставленного без внимания рецензентов: Расчеты по E.Kaplan-P.Meier, во всех их модификациях, завышают показатели выживаемости и приводят к наибольшим, сравнительно с иными методами, расхождениям между расчетными и фактическими данными.
В этой связи, как понимать авторов рецензии, назвавших иные методы грубыми, а «настоящую оценку Каплана -Майера» более точной?
Вопрос рецензентов N2
Корректно ли обращаться напрямую к аудитории врачей-исследователей, декларируя, что твой метод лучше классических, минуя специалистов в области математической статистики?
Авторы рецензии рекомендуют «стандартный путь изобретения и внедрения» для новых методов статистического анализа. Предложенная ими последовательность указана в левой части составленной нами таблицы, реализация полученных указаний отражена в правой:
Что из проделанного оказалось некорректным?
В связи с сомнениями авторов рецензии в выборе «лучшего» метода расчетов (т.е., более надежного в плане соответствия актуариальных и действительных данных) возможно. обратиться к Табл.2 нашей статьи (См Табл. 5-2; с.54 этой книги). Во всех шести реальных, репрезентативных выборках, к тому же различных по прогнозу выживаемости, предложенный нами метод показал наибольшее соответствие расчетных и фактических показателей.
Вопрос рецензентов N3, связанный с предыдущим
Прошел ли метод серьезную математикостатистическую экспертизу?
Фактический материал изложен в ответе на предыдущий вопрос. Пользуясь случаем, счастливо представившимся после прочтения рецензии, авторы статьи были бы признательны за информацию о том, кого из перечисленных выше авторитетных специалистов, дававших оценку методу, авторы рецензии признают «единственным рецензентом-экспертом»?
Вопрос рецензентов N4
Реализован ли метод в виде простого алгоритма или программы удобной и понятной пользователю?
Не вдаваясь в подробности отметим, что наш метод определяет показатель выживаемости контрольного срока (Pi) отношением числа выживших (переживших контрольный срок; n’i) и числа выбывших (но вероятно доживущих до контрольного срока; wi), умноженного на вероятность этого дожития (pi), к общему числу наблюдений (n):
(формула2)
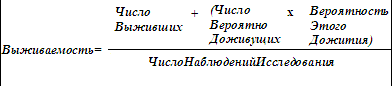
Формула (2) отражает алгоритм метода и приводится для наиболее простого ответа на поставленный вопрос. Определение вероятности дожития выбывших больных до контрольного срока (pi), вместе с определением показателя выживаемости контрольного срока (Pi) может быть проведено итеративным методом, в системе двух уравнений. Такое проведение расчетов и самое главное – объяснение принципов нашей методики – не требует применения специальных математических знаний и понятно специалистам - онкологам.
Рецензируя метод, д.т.н., проф. О.М.Дукарский предложил иное, более удобное для проведения вычислений решение. Показатель выживаемости контрольного срока (Pi) определяется по формуле (3), где “d” – число умерших.
(формула3)
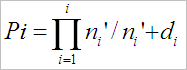
Примером может быть расчет 1-5-летней выживаемости в выборке из 10 наблюдений, данные о которых указаны в приводимой ниже “таблице дожития”:
| i-(i+1) | n | d | w | n’ |
|---|---|---|---|---|
| 0-1 | 10 | 3 | 2 | 5 |
| 1-2 | 5 | 0 | 1 | 4 |
| 2-3 | 4 | 1 | 1 | 2 |
| 3-4 | 2 | 0 | 0 | 2 |
| 4-5 | 2 | 0 | 1 | 1 |
Расчет проводится несколькими арифметическими действиями: Р5=(5/ 5+3) (4/ 4+0) (2/ 2+1) (2/ 2+1) (1/ 1+0)Таким образом, показатели 1-5-летней выживаемости соответ-ствуют: 0,625; 0,625; 0,417; 0,417; 0,417.
Изложенное дает основания авторам статьи полагать, что метод действительно реализован в виде простого алгоритма - т.е. программы действий, удобных и понятных пользователю.
Теперь о формулировке авторов рецензии их собственного ответа на их же собственный вопрос. Цитируем: «Предлагаемый метод излагается как итеративный, хотя рецензент Дукарский указал точную и простую прямую формулу. Проводить вручную (программа автором не предлагается) последовательные вычисления, когда есть совсем простая формула – более чем странно».
Действительно, более чем странные фразы. Вначале авторы рецензии спрашивают о том, реализован ли метод в виде простого алгоритма или удобной и понятной программы, а затем констатируют, что точная и совсем простая формула (она же – алгоритм и программа вычислений) все таки есть. Снимается ли таким образом вопрос рецензентов-4? Для нас, авторов статьи, претендующих на ее публикацию в Вашем уважаемом журнале, это имеет существенное значение, поскольку, как считают рецензенты, достаточно отрицательного ответа хотя бы на один поставленный вопрос для отрицательной оценки всей нашей статьи.
В этой связи, полагаем, Вами будет правильно понято наше стремление дать подробную, исчерпывающую информацию по всем возникшим вопросам.
Вопрос рецензентов N5
Корректно ли выбраны для сравнения и описаны другие методы анализа выживаемости, обоснована ли методика сравнения эффективности?
Отвечая цитируем собственную статью, раздел «материалы и методы»: Актуариальные расчеты выполнены в шести группах больных тремя традиционными методами (по А.М.Меркову, S.Сutler-F.Ederer, E.Kaplan-P.Meier), а также по нашей модификации.
Данные о составе выборок представлены в таблице (См Табл.5-1; 5-2; 5-3 этой книги). Для суждения о надежности актуариальных расчетов в анализируемых выборках определены наибольшие и наименьшие показатели 1-5-летней выживаемости - как возможные, если бы все наблюдаемые и выбывшие дожили до 5 лет или напротив, умерли до этого контрольного срока. Фактические показатели исчислены после 5 лет наблюдения. В статье также указано, что оценка надежности метода выполнена путем сопоставления актуариальных и фактических показателей. Результаты- в этой книге - указаны в Табл.5-2 и на Рис.5(1-3).
В чем может состоять «некорректность» применения традиционных методов анализа выживаемости? Если эти методы приводят к не совсем корректным результатам (заниженным или завышенным) то это, как представляется:
- подтверждает преимущества предлагаемой методики (в наших расчетах проявляется тенденция к получению результатов выше заниженных, но ниже завышенных и более всего соответствующих фактическим);
- указывает пользователям-держателям современных компьютерных пакетов SAS на те (не совсем совершенные) методические принципы, по которым работают их программы;
- побуждает этих немногих пользователей, как и кратно большую аудиторию врачей- исследователей, указанных пакетов не имеющих, обратить наконец внимание на соответствие действительности тех показателей, что публикуются в литературе со ссылками: «рассчитано по Kaplan-Meier, (1958)» и вообще «рассчитано актуариальным методом».
Если обозначенная проблема достаточно серьезна и для ее решения требуются дополнительные исследования с последующей публикацией в специализированном статистическом журнале, то авторы статьи предлагают свое сотрудничество специалистам по математической статистике, согласным с изложенной нами концепцией. Однако обсуждение достоверности актуариальных расчетов (что предусматривает сравнение расчетных и фактических данных), полагаем, возможно и без выхода в свет специальной математической публикации, именно в аудитории врачей- исследователей,. для которых эти расчеты и предназначены.
Правда, отечественные специалисты недостаточно знакомы с актуариальными расчетами. В таком ведущем издании, как Российский Онкологический журнал, например, за 3 (неполных) года всего в 3 статьях сообщается о применении этих вычислений –в одной по S.Сutler-F.Ederer, в рекомендательном изложении экспертов ВОЗ (1979) и в 2 -по E.Kaplan-P.Meier. Западный же опыт 40-летнего применения «расчетов по таблицам дожития» побудил (именно клиницистов) усомниться в достоверности актуариальных расчетов: “Actuarial 5-year survival estimates: Can we trust them?” (J.Thorac. Cardovasc. Surg. 1990; 100:455-65). Дискуссия в зарубежной литературе насыщена поучительными сведениями от привлеченных специалистов по информатике (и удивительным образом выдержана в исключительно благожелательной тональности). Напротив, наш отечественный аналог подобной дискуссии, которым могло бы стать предложенное авторами рецензии сравнение эффективности анализируемых актуариальных методов, как представляется, не оправдал возлагавшихся ожиданий.
Авторы рецензии игнорируют правомерность нашего сопоставления результатов, полученных при расчетах разными методами в одной выборке. Рецензирование представленных нами материалов заменено их собственным сравнением актуариальных методов посредством алгебраического преобразования формул расчетов. Это сравнение закончено выводом о невозможности применения двух методов из четырех, а наш метод отвергнут (как не-актуариальный и ошибочный) в следующем разделе. Естественно, нам есть что возразить рецензентам:
Из сопоставлений исключен метод А.М.Меркова, как устаревший и сугубо эмпирический. Но ведь все традиционные методы опубликованы почти одновременно, в 1958 году. Следует ли в таком случае считать современными расчеты остальных авторов? Кроме того, разве L’=(u+w)/2 по S.Сutler-F.Ederer не является эмпирической оценкой (сравнительно с L’={L+[L-(d+u+w)]}/2 по А.М.Меркову)? Условия, при которых метод А.М.Меркова неприемлем, известны. Они указаны не только в нашей работе. (См., например: В.В.Двойрин, А.А.Клименков. Методика контролируемых клинических испытаний. М., 1985) Но ведь при некоторых иных, указанных в нашей статье условиях, применение «устаревшего» метода А.М.Меркова приводит к получению результатов более приближенных к фактическим, чем расчеты наших современников S.Сutler-F.Ederer, E.Kaplan-P.Meier. Почему же ее, оценку А.М.Меркова «нельзя рассматривать всерьез» ?
Исключение авторами рецензии из сравнения эффективности анализируемых актуариальных расчетов и метода E.Kaplan-P.Meier стало полной неожиданностью для нас, авторов статьи. Важность последующих положений обуславливает необходимость краткого пояснения. В статье, направленной в Российский Онкологический журнал, указаны результаты расчетов по "Actuarial approximation of the PL-Estimate". Дополнительно проведены расчеты по "PL-Estimate". В этой книге они указаны в Табл.5-3(А;Б;В). Все они подтверждают завышение результатов по E.Kaplan-P.Meier. Особо отметим, что указанные модификации метода E.Kaplan-P.Meier основаны на одних и тех же формулах. Следовательно, взяв для сравнения эффективности как бы «грубую» актуариальную формулу, авторы рецензии проделывали свои преобразования и над получившей их высокую оценку «точной и настоящей» формулой Каплана-Майера, основой продукт-лимит анализа. Заслуживают особого разъяснения последующие действия авторов рецензии: ими взятая и преобразованная формула метода E.Kaplan-P.Meier затем ими же и отвергнута, так как она дает заниженную оценку смертности. То есть, в иной (нашей) терминологии – завышает выживаемость. Казалось бы, сделанное врачами-исследователями заключение о том, что применение метода E.Kaplan-P.Meier сопряжено с искажением выживаемости, обусловливает прямые показания к тому, чтобы специалисты в области математической статистики представили свой авторитетный анализ этих расчетов. Однако метод, вызвавший множественные вопросы, оказывается исключенным из сопоставлений. Почему же: «Использование ее (т.е. оценки Каплана-Майера) в анализе таблиц дожития – неграмотно, дискредитирует и метод и оценку в глазах конечных пользователей»? Представляется, что применение данного метода может засвидетельствовать конечным пользователям о возможности искажений результатов расчетов. Именно об этом сказано в нашей статье. Каким образом констатация завышения результатов может дискредитировать анализ остается недоступной пониманию. Кроме того, мы, как конечные пользователи, имея право рассчитывать на серьезную математико- статистическую экспертизу предложенных для публикации положений, естественно не получили удовлетворения от предложенных взамен всего лишь элементарных алгебраических выкладок.
Таким образом, по нашему мнению, авторы рецензии не дают обоснованной критики нашего методического подхода к решению задач исследования и не представляют доказательств, опровергающих полученные в нашей работе результаты.
Вопрос рецензентов N6
Является ли предлагаемый метод действительно новым и более эффективным по сравнению с классическим методом обработки таблиц дожития?
Наша статья дает положительные ответы на поставленные вопросы.
Аргументация иного заключения рецензентов основывается лишь на анализе выведенных ими формул для оценки смертности (показателя «q», кстати не востребованного ни в расчетах по E.Kaplan-P.Meier ни в предложенном нами методе). Их утверждение, что при нашем анализе «…просто исключаются цензурированные наблюдения» (т.е. выбывшие больные, вероятно доживущие до контрольного срока), а также, что нового метода обработки таблиц дожития не предложено вообще, означает что формулы (2) также вообще не существует. Тем не менее, в формуле нашего метода:
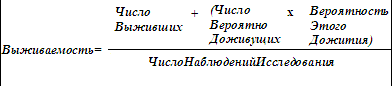
Возможно отметить действительно новый (т.е. не применявшийся ранее), оригинальный (т.е. чуждый подражательности) подход к обработке censored survival information, что с очевидностью позволяет идентифицировать данный метод расчетов именно как актуариальный. (Актуариальный расчет = определение выживаемости с учетом возможности дожития до контрольного срока больных с вероятностными сведениями о продолжительности жизни – т.е. выбывших из наблюдения и наблюдаемых, но еще не доживших до анализируемого срока.) Материалы статьи, направленной в Ваш журнал, подтверждают концепцию большей эффективности (надежности) оценки продолжительности жизни именно благодаря изложенной выше методике учета вероятности дожития.
К сожалению, (следует откровенно это признать), метод не вполне выдержал проверку в экстремальных условиях, которыми возможно считать пример, иезуитски предложенный авторами рецензии: “n=100, d=1, w=99”. Иными словами, в группе из 100 больных (ni =100) в интервале от «i» до «i+1» в 1 случае наступил летальный исход, остальные 99 еще не дожили до контрольного (i+1) срока. Авторами рецензии фактически спрашивается, как можно определить показатель продолжительности жизни в срок, до которого еще не дожил ни один больной. Подобной задачи не ставилось ни в одном из актуариальных методов. Напротив наличие (любого) числа наблюдений в конце интервала является обязательным условием расчетов «по таблицам дожития». См. также главу IV в этой книге. Очевидно, что в предложенном примере выживаемость в срок «i+1» просто не может быть определена из-за незавершенности срока наблюдения и фактического отсутствия числа наблюдений в конце интервала, в срок «i+1», то есть, ввиду отсутствия субстрата расчетов. Попытка же определения выживаемости не имеет какого либо обоснования и может быть квалифицирована как вычисления в абсурдно созданных (к.т.н. С.М.Куликов и д.м.н., проф. В.Г.Сав-ченко) условиях.
Естественно, что результаты, полученные в этих условиях, по праву оцениваются этими авторитетными специалистами именно как абсурдные. Таковыми совершенно справедливо являются как Р=0, рассчитанный по формулам нашего метода, так и 0,98?P?0,99 вычисленный по формулам иных методов. (Для тех, кого приведенная аргументация не убеждает, возможно пояснить на примере аналогии: выписано сто больных, один умер. Спрашивается, сколько из оставшихся 99 доживут до две тысячи сотого года…) Хотя эмоционально оценка «Р=0» воспринимается «более точной» – мол, поскольку выживаемость в данный срок не определяется, то она адекватна нулевому показателю, и совсем не соответствует гарантированному на 99% долгожительству.
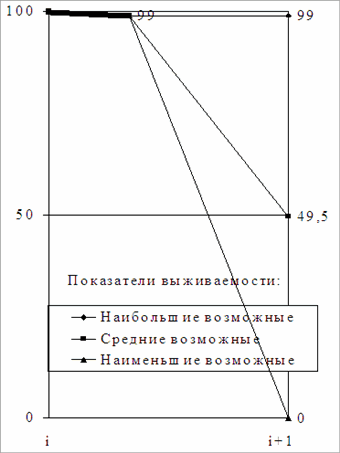
Определение выживаемости в примере из 100 наблюдений
Условия расчетов:
n=100, d=1, w=99
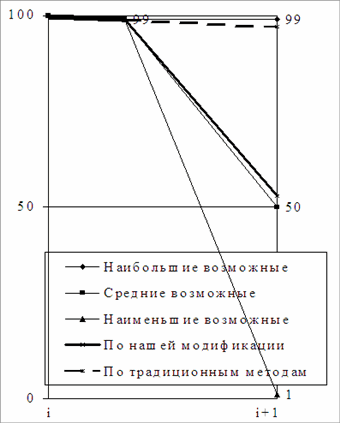
n=100, d=1, Sv=1, w=98
Между тем, абсурдность результата в рассмотренном примере ставит под сомнение суть всего рецензируемого материала и приводит к заключению о том, что «статья не может быть принята к публикации».
Однако мы, авторы статьи, обосновав не реалистичность обсуждаемого примера, считаем возможным усомниться и в правомочности умозаключений, сделанных на этой основе авторами рецензии. Поэтому, просим еще раз вернуться к примеру рецензентов, вынужденно анализируемому вместо 6 наших, представленных в статье, но отвергнутых рецензентами выборок. Это может быть признано оправданным в случае рассмотрения наших разногласий с авторами рецензии при принятии итогового решения.
Условия примера: “n=100, d=1, w=99” (в нашем определении: --/99/100; Рис. на с.141, слева), позволяют лишь констатировать, что выживаемость в срок «i+1» может составить от 0 до 99% если до окончания анализируемого интервала не доживет никто, либо доживут все 99 больных с вероятностным прогнозом дожития. Средний возможный показатель выживаемости в данной группе соответствует 49,5%. Более информативного анализа выполнить по данному примеру, выражаясь сухо и не эмоционально, «не представляется возможным».
Но предложим единственное изменение условий примера - один больной все же доживает до конца интервала. Тогда: “n=100, d=1, Sv=1, w=98” (в нашем определении: 1/98/100; Рис. на с.141, справа). В этом случае появляются и возможности для более определенных суждений. Выживаемость может составить от 1 до 99% при среднем возможном показателе 50%. Традиционные актуариальные расчеты в новой выборке показывают 99% выживаемость, что представляется безусловно завышенным результатом. Напротив, наша модификация предполагает несколько более реалистичную возможность 50±5% выживаемости, что совпадает со средним ожидаемым показателем.
В случае большей определенности условий, а именно – при уменьшении пропорции вероятностных данных до 1/ 3 – 1/ 2 (см. обоснование целесообразности в главе IV), выборка приняла бы вид: хх/33/100 или хх/50/100. Это неизбежно привело бы к уточнению ее остальных параметров и определило бы число переживших контрольный срок «хх». Число, скрытое за параметром «хх» позволило бы судить о прогнозе дожития для 33-50 случаев еще не доживших до контрольного срока. Дальнейшие рассуждения о показателе выживаемости в указанной выборке, а также о достоверности его определения актуариальными методами, стали бы аналогичны представленным в статье, направленной в Ваш журнал.
Представляется, что в случае подобных, даже совсем не алгебраических преобразований выборки, возможно было бы обойтись и без затребованных компьютерных экспериментов в статистическом Монте-Карло.
Заключение
В нашей работе показано, что традиционные актуариальные расчеты, ввиду несовершенства их методических принципов, могут искажать реальность; что предложенный нами метод более корректный и точный; что наши положения подтверждаются практикой вычислений.
В рецензии безосновательно отвергнута правомочность сопоставления результатов анализируемых методов, наш метод бездоказательно объявлен ошибочным, а результаты расчетов не приняты к рассмотрению вообще.
Возможно констатировать, что таким образом оставлен открытым вопрос-3 о том, прошел ли метод серьезную математико-статистическую экспертизу. Если конечно считать таковой текст указанных выше рецензентов.
кандидат мед. наук С.М.Волков, старший научный сотрудник ОНЦ им.Н.Н.Блохина с соавторами
Июль –август, 1988г.



